
Faust 101 for the confined
The covid-19 containment gives us at least one excellent opportunity to train! If you've always wanted to get into Faust programming but didn't have the time, here's your chance!
The objective of this workshop is to help you get familiar with the Faust language through very simple examples of signal processing and sound synthesis. The documentation and the examples we will use can be found here:
All examples will be run in the online Faust IDE:
If ever the sounds produced with the IDE are of poor quality, with some clicks, one can use the online editor, which is more rustic, but also lighter:
Faust in a few words
- Faust is a Domain-Specific Language for real-time signal processing and synthesis (like Csound, Max/MSP, SuperCollider, PureData,. . . ).
- Faust is based on purely functional approach.
- a Faust program denotes a signal processor: a function that maps input signals to output signals.
- Programming in Faust is essentially combining signal processors using an algebra of 5 composition operations:
<: :> : , ~. - Faust is a compiled language, the role of the Faust compiler is to synthesize the most efficient implementations.
- Faust offers end-users a high-level alternative to C/C++ to develop audio applications for a large variety of platforms.
Part 1: Very simple examples

Let's start with some simple examples of Faust programs.
Example 1: The simplest Faust program
This is the simplest Faust program imaginable. It contains only one line of code, the definition: process = _;. This program copies the audio input to the audio output.
Let's try this program using the online Faust IDE:
Several lessons can be learned from this very simple example:
- a Faust program has at least one definition, that of the keyword
processwhich indicates the entry point of the program. - a definition always ends with a
;. A common mistake is to forget the semicolon at the end of a definition. - the
_sign represents one of the primitives of the language (primitives are the predefined functions of the language). It represents an audio cable that lets the signal pass through without transforming it. This is what one calls in mathematics the identity function, the signal that enters on the left comes out on the right identically.
Example 2: Adding two signals
We saw in the previous example the primitive _. Faust has a large number of primitives, including all mathematical operations.
The + primitive for instance is used to add two signals. It can therefore be used to transform a stereophonic signal (on two channels) into a monophonic signal as in the following example:
Example 3: Multiplying two signals
The * primitive for instance is used to multiply two signals:
As you can hear, multiplying the two channels of a signal between them transforms the sound quite drastically.
Example 4: Parallel composition
Programming in Faust consists in assembling primitive operations to form more or less complex audio circuits. To realize these assemblies, Faust has 5 composition operations: ~, ,, ;, <:, :>.
Let's first look at the parallel composition represented by the comma ,:
We made a stereo cable and when we play the audio file, we now hear it on both speakers.
It is very important to distinguish between primitives, such as _, + or *, and composition operations such as , or :. Primitives represent operations on audio signals, whereas composition operations are used to link two audio operations together. In other words, you can write + or * alone, because they represent valid audio operations, but you can never write , or : alone because they are used to connect two audio operations. You must always write A,B or A:B.
The primitives of Faust are organized in several categories. We find all the numerical functions of the C language, but applied to audio signals:
| Category | Primitives |
|---|---|
| Arithmetic | +, -, *, /, ... |
| Comparison | <, ==, !=, <=, ... |
| Trigonometric | sin, cos, ... |
| Log and Co. | log, exp, ... |
| Min, Max | min, max, ... |
| Selectors | select2, select3, ... |
| Delays and Tables | @, rdtable, ... |
| GUI | hslider(), button(), ... |
Here is a summary table of the five composition operators:
| Syntax | Priority | Association | Description |
|---|---|---|---|
A ~ B |
4 | left | Recursive Composition |
A , B |
3 | right | Parallel Composition |
A : B |
2 | right | Sequential Composition |
A <: B |
1 | right | Split Composition |
A :> B |
1 | right | Merge Composition |
Example 5: Controlling the volume
Let's see an example where we combine three primitives:
_, 0.1 and *,
with two composition operators:
, and :.
The idea here is to lower the volume of the incoming signal to one tenth of its initial value. This is done by multiplying the incoming signal by 0.1:
Note that we have used parentheses in this example to clearly mark the order in which things should be done. We start by putting _ and 0.1 in parallel, and then compose them in sequence with *.
But, just as in (2*3)+7 were the parentheses are not really necessary because multiplication takes precedence over addition, one could write directly process = _,0.1 : *; without the parentheses, because parallel composing takes precedence over sequential composing. The priority of the composition operators is shown in the previous table.
Example 6: Controlling the volume with a slider
Instead of controlling the volume by editing the code, it is far more convenient to use a graphical slider. For that purpose we can use a hslider(...), a horizontal slider. It takes five parameters. The first one is the name "volume", then we have the defaut value 0.1, the minimun value 0, the maximum value 1 and a step value 0.1. So here the default value is 0.1:
Example 7: Mono Amplifier
We have written very simple programs so far, that fit into one line of code. We will now introduce additional definitions. A definition should be understood as a way of giving a name to something, which saves us from typing the definition every time and makes the program easier to understand:
Example 8: Stereo Amplifier
Continuing in the same vein, we will define a stereo amplifier as two mono amplifiers in parallel:
Note that even if the hslider volume appears several times in our code, there will only be one in the user interface:
Example 9: Vertical sliders
Instead of horizontal sliders, we could use vertical sliders. Just replace hslider(...) with vslider(...):
Example 10: Knobs instead of sliders
By default sliders are ... sliders! You can change their appearance by using the metadata mechanism.
Metadata is information that you put in square brackets in the slider name. For example the metadata "...[style:knob]..." allows you to turn the slider into a rotary knob:
Example 11: Syntactic sugar
We have used the core syntax of Faust so far. For example to multiply the incoming signal by 0.1, we wrote _,0.1:*. For numerical expressions this notation is not always the most convenient and sometimes we would prefer to use the more traditional infix notation and write instead _*0.1. We can also use the prefixed notation and write *(0.1).
Let's rewrite the definition of the monoamp using the prefix notation:
Here is a table of equivalent notations, with the same expression in all three syntaxes. Keep in mind that infix and prefix expressions are translated to core syntax:
| Expression | Description |
|---|---|
_,0.1:* |
core syntax |
_*0.1 |
infix notation |
*(0.1) |
prefix notation |
These notations can be freely combined. For example, the following expressions are all equivalent:
| Expression | Description |
|---|---|
*(1-m) |
prefix + infix notation |
_*(1-m) |
only infix notation |
_,(1,m:-):* |
core syntax |
Example 12: A mute button
We would like to be able to mute the sound completely at the touch of a button, without having to change the volume.
Let's add a mute stage to our mono amplifier. In order to mute the signal we just have to mutiply it by 0. We will use for that purpose a checkbox(...), a user interface element that produces a signal which is 0 by default and 1 when it is checked. As we want to multiply the signal by 0 when the checkbox is checked we will use 1-checkbox("mute"):
Example 13: Vertical and horizontal Layout
As can be seen in the previous example, by default, the layout of the elements is vertical. You can change this layout by using hgroup(...) and vgroup(...). For example to make the layout horizontal you can write:
s
Example 14: Differentiate the volume of the two channels
To differentiate the volume control of our two channels, we will parametrize monoamp with a channel number c which will be used to differentiate the name of each volume control. Note that the name c of the parameter must only have one letter to be well interpreted in the slider name "volume %c[style:knob]":
Example 15: Having many channels
We have built a stereo amp, but suppose we wanted to generalize this construction to an arbitrary number of channels. To do so, we will introduce the par(i, N, ...) construction which allows us to put several times an expression in parallel. It is in a way the equivalent of the for() loop of a classical programming language.
In our case we want to indicate the number of channels of our amplifier:
Part 2: Delays and Feedbacks
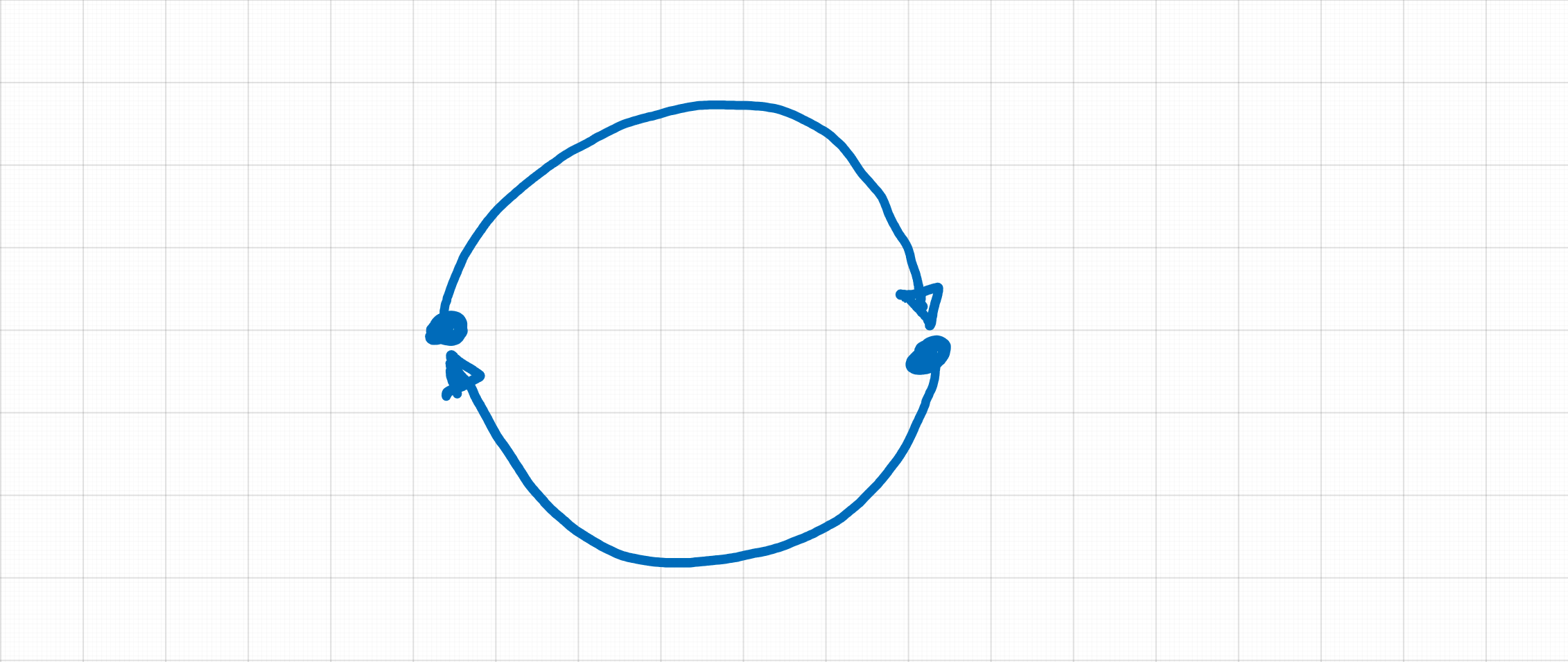
In this new section we will see two important notions, that of delay with the @ primitive, and that of feedback (from a looped circuit) which will require the use of the recursive composition A~B which allows to loop the outputs of A into the inputs of B, and the outputs of B into the inputs of A.
Example 1: Monophonic delay of 1 second
Let's start with a very simple example, a monophonic delay of 1 seconds or 44100 samples. We will use the prefix notation:
Example 2: Delay of 0.1 second on the right channel
To hear the delay better, let's put it only on the right channel and leave the left channel unchanged:
Example 3: the bouncing of sound on a wall
By combining a delay and an attenuation we can simulate the bouncing of sound on a wall:
Example 4: A simple monophonic echo
To simulate an echo, all we need to do is create a feedback loop. We'll use the recursive composition A~B:
Example 5: A stereophonic echo
Let's make a stereophonic echo with two monophonic echos in parallel:
Example 6: Adding parameters
We will now generalize our echo with parameters to control its duration and feedback level:
Example 7: Slider for the feedback control
We can now add a slider to control the level of feedback:
Example 8: Freeze effect
We would now like to prevent the sound level from rising indefinitely when we set the feedback level to 1. The idea is to gradually shut down the input when the feedback level exceeds a certain threshold:
Part 3: Basic Oscillators
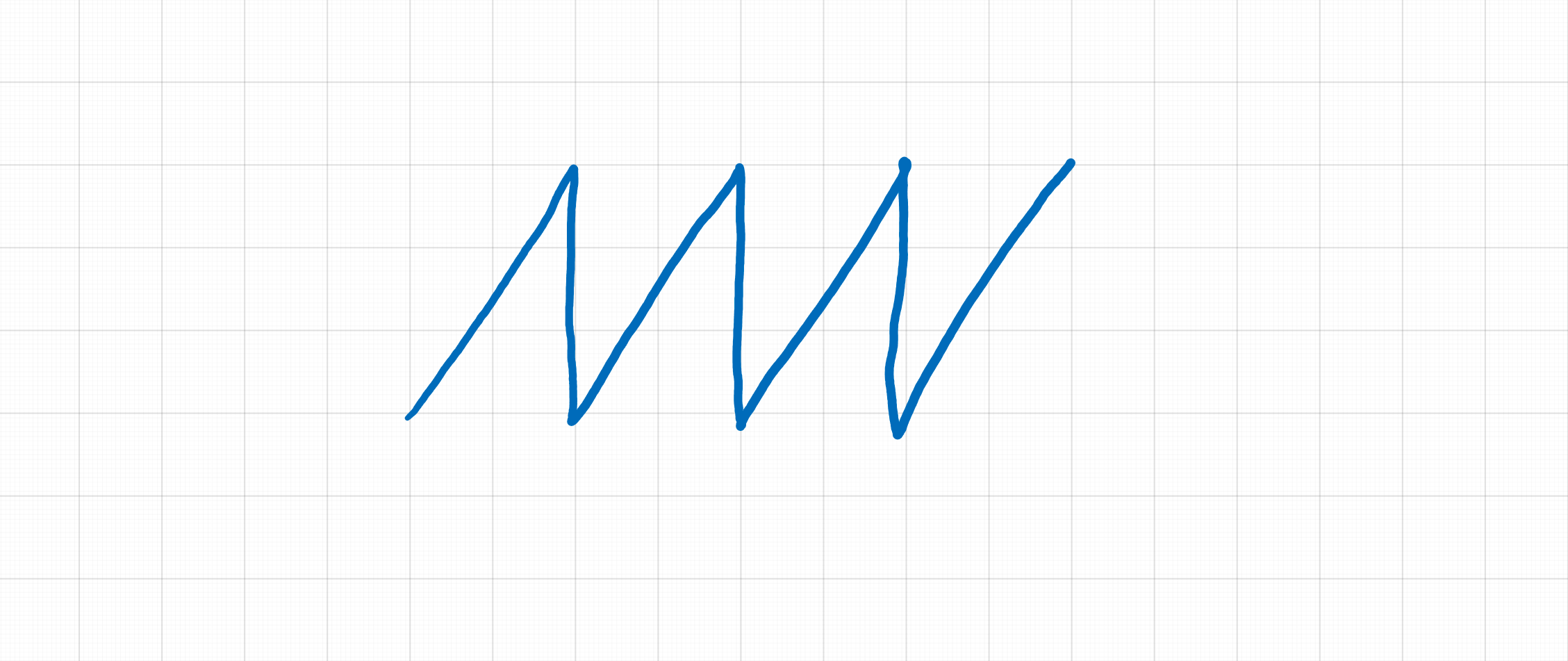
By convention, in Faust, a full-scale audio signal varies between -1 and +1, but we will first start with a sawtooth signal between 0 and 1 which will then be used as a phase generator to produce different waveforms.
Phase Generator
The first step is to build a phase generator that produces a periodic sawtooth signal between 0 and 1. Here is the signal we want to generate :
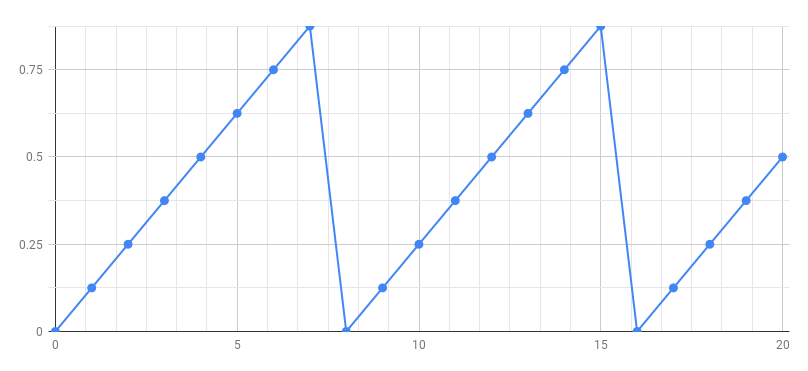
Example 1: Ramp
To do this we will produce an "infinite" ramp, which we will then transform into a periodic signal thanks to a part-decimal operation:
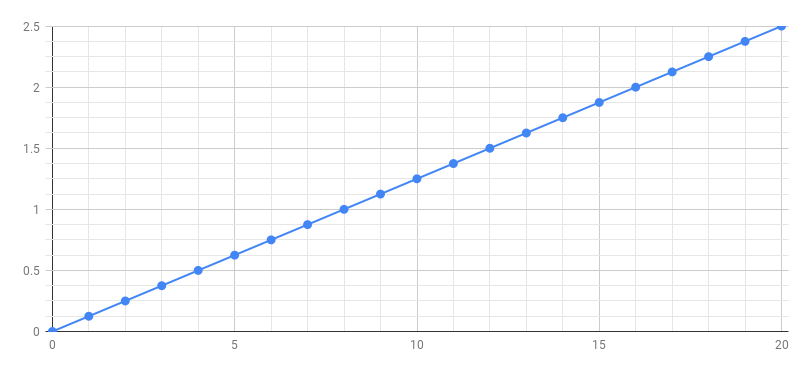
The ramp is produced by the following program:
Semantics
To understand the above diagram, we will annotate it with its mathematical semantics:
As can be seen in the diagram, the formula for the output signal is:
We can calculate the first values of :
- .
- .
- ...
- ...
Example 2: a phase signal
How do I turn the above ramp into a sawtooth signal? By deleting the whole part of the samples in order to keep only the decimal part: .
Let's define a function to do this:
decimalpart(x) = x - int(x);
We can now use this function to turn our ramp into a sawtooth. It is then tempting to write:
process = 0.125 : + ~ _ : decimalpart;
From a mathematical point of view, that would be perfectly correct, but we will accumulate rounding errors. To keep total accuracy, it is better to place the operation of the decimal part inside the loop, like this:
process = 0.125 : (+ : decimalpart) ~ _;
We can now try the whole code (think about turning down the volume) :
In our definition of phase, the value of the step, here 0.125, controls the frequency of the generated signal. We would like to calculate this step value as a function of the desired frequency. In order to do the conversion, we need to know the sampling frequency. It is available in the standard library as ma.SR and will be setup at start time by the underlying audio layer. To use this standard library we add the following line to the program: import("stdfaust.lib");.
Suppose we want our phase signal to have a frequency of 1 Hz, then the step should be very small 1/ma.SR, so that it takes ma.SR samples (i.e. 1 second) for the phase signal to go from 0 to 1.
If we want a frequency of 440 Hz, we need a 440 times larger step so that the phase signal goes from 0 to 1, 440 times faster:
phase = 440/ma.SR : (+ : decimalpart) ~ _;
This definition can be generalized by replacing 440 with an f parameter:
phase(f) = f/ma.SR : (+ : decimalpart) ~ _;
and changing the desired frequency to phase:
process = phase(440);
Example 3: Sawtooth signal generator
We can now use the phase generator to produce a sawtooth signal:
Example 4: Square wave generator
We can also use the phase generator to produce a square wave signal:
Part 4: Additive synthesis

Example 1: sine wave generator
The phase generator is also the basis of the sine wave generator:
But now that we have seen how to create a sinusoidal oscillator from scratch, we will use the one defined in the standard Faust libraries:
Example 2: a sine wave with volume control
In this second example we used a horizontal slider hslider(...) to control the sound level:
The first parameter is a string that indicates the name of the slider. It is followed by four numeric parameters. The second parameter 0.1 indicates the default value of the slider, i.e. the value that the slider will deliver when the program is started. Then we have the minimum value 0, the maximum value 1 and the variation step 0.01.
Example 3: Exercise, add a frequency control
As an exercise, replace, in the previous example, the frequency 440 by a horizontal slider whose name will be freq, the default value 110, the minimum value 40, the maximum value 8000 and the step 1:
Example 4: Frequency aliasing phenomenon beyond SR/2
A well known problem in the field of digital sound synthesis is frequency aliasing: any frequency beyond half the sampling frequency is folded in the audible spectrum:
Example 5: Additive synthesis
An example of an additive synthesis, where the level of each partial can be set individually:
Note the use of the sum(i, n, foo(i)) construction which is equivalent to foo(0)+foo(1)+...+foo(n-1).
Example 6: Approximation of a square signal by additive synthesis
We saw earlier how to produce a perfect square wave signal. This perfect square signal contains an infinite number of harmonics which, due to sampling, will fold over the audible spectrum, resulting in a less accurate, noisy sound! A square signal can be approximated by additive synthesis, by adding an infinite series of odd harmonics (see https://en.wikipedia.org/wiki/Square_wave):
As an exercise, change the number of harmonics to see the approximation improve (but do not exceed SR/2).
Example 7: Approximation of a sawtooth signal by additive synthesis
Similarly, a sawtooth signal can be approximated by additive synthesis, by adding an infinite series of harmonics (see https://en.wikipedia.org/wiki/Sawtooth_wave):
Example 8: Band limited oscillators
The problem of aliasing can be solved using band-limited oscillators available in Faust libraries:
Part 5: Subtractive synthesis
Subtractive synthesis is the opposite of additive synthesis. It consists in starting from a rich sound, for example white noise, and sculpting its spectrum.
Example 1: a white noise
A white noise generator:
Example 2: lowpass
Here the noise sound is filtered with a low-pass filter that removes frequencies lower than a selected cutoff frequency:
The used fi.low filter can be defined with an argument that modifies the frequency attenuation slope.
Example 3: high pass
Here the noise sound is filtered with a high-pass filter that removes frequencies higher than a selected cutoff frequency:
The used fi.highpass filter can be defined with an argument that modifies the frequency attenuation slope.
Example 4: bandpass
By combining a low-pass and high-pass filter in sequence, a bandpass filter that removes frequencies lower than a selected low cutoff frequency, and higher than a selected high cutoff frequency, can be defined (using the already described fi.lowpass and fi.highpass filters):
Example 5: resonant
A resonant filter amplifies a selected frequency range:
The used fi.resonlp filter has an argument to select the desired frequency, a Q factor to shape the frequency range, and a gain factor.
Example 6: fir
Here a FIR filter is used:
Example 7: iir
Here a IIR filter is used:
Example 8: comb filter
A comb filter attenuates a set of consecutives frequency bands:
Example 9: Karplus Strong (1/2)
Example 10: Karplus Strong (2/2)
Example 11: Kisana
Part 6: Synthesis by frequency modulation
Example 1: frequency modulation
Example 2: frequency modulation with envelops
Further readings
The documentation of Faust libraries is available here:
