Building a Simple MIDI Synthesizer

We are going to build a MIDI synthesizer from scratch (without using the Faust libraries).

Phase Generator

The first step is to build a phase generator that produces a periodic sawtooth signal between 0 and 1. Here is the signal we want to generate:

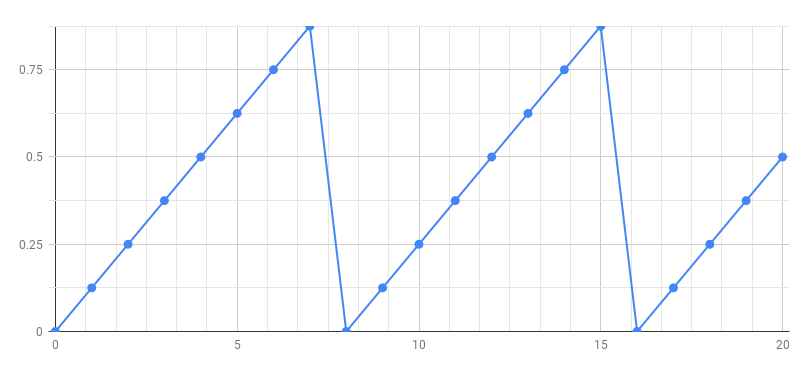
Ramp

To produce the above signal, we must first generate a ramp signal

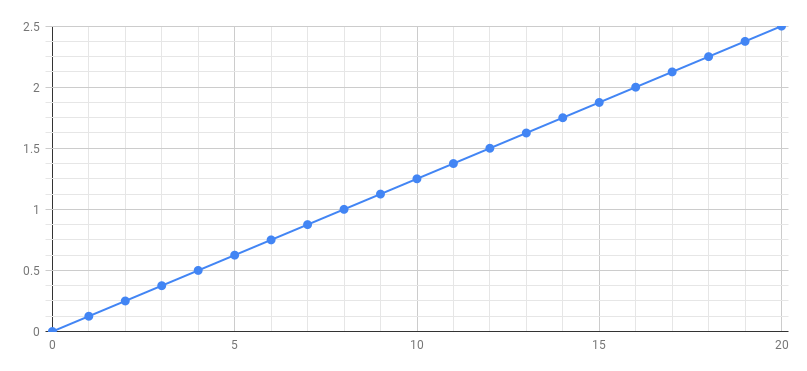
using the following Faust program:

You can think of a Faust program as a description of an audio circuit where 0.125, + and _ are primitives of the language (predefined elementary audio components), and the other two signs: : and ~ are used to connect these audio components together.

Semantics

To understand the above diagram let's annotate it with its mathematical semantics.

As we can see in the diagram, the formula of the output signal is: $y(t) = y(t-1) + 0.125$

We can compute the first values of $y(t)$:

• $y(t<0)=0$
• $y(0) = y(-1) + 0.125 = 0.125$
• $y(1) = y(0) + 0.125 = 2*0.125 = 0.250$
• $y(2) = y(1) + 0.125 = 3*0.125 = 0.375$
• ...
• $y(6) = y(5) + 0.125 = 7*0.125 = 0.875$
• $y(7) = y(6) + 0.125 = 8*0.125 = 1.000$
• $y(8) = y(7) + 0.125 = 9*0.125 = 1.125$
• ...

Phase Signal

How can we transform the above ramp into a sawtooth signal? By removing the integer part of the samples in order to keep only the decimal (fractional) part (3.14159 -> 0.14159).

Let's define a function to do that:

decimalpart(x) = x - int(x);

We can now use that function to transform our ramp into a sawtooth. It is then tempting to write:

process = 0.125 : + ~ _ : decimalpart;

From a mathematical point of view that would be perfectly correct, but we will accumulate rounding errors. To keep full precision it is better to place the decimal part operation inside the loop:

process = 0.125 : (+ : decimalpart) ~ _;

We can now listen to the produced signal. Just copy and paste the decimalpart and process definitions into the Faust Web IDE.

Controlling the Frequency of the Phase Signal

Let's first rearrange our code:

In our phase definition the step value, here 0.125, controls the frequency of the generated signal. We would like to compute this step value according to the desired frequency. In order to do the conversion we need to know the sampling rate. It is available from the standard library as ma.SR.

Let's say we would like our phase signal to have a frequency of 1 Hz; then the step should be very small, 1/ma.SR, so that it will take ma.SR samples (i.e. 1 second) for the phase signal to reach 1.

If we want a frequency of 440 Hz, we need a step 440 times bigger so that the phase signal reaches 1 four hundred and forty times faster.

phase = 440/ma.SR : (+ : decimalpart) ~ _;

We can generalize this definition by replacing 440 by a parameter f:

phase(f) = f/ma.SR : (+ : decimalpart) ~ _;

and by indicating the desired frequency when we use phase:

process = phase(440);

Creating a Sine Wave Oscillator

The next step is to transform the phase generator above into a sine wave generator. We will use the sin primitive that computes the sine of x (measured in radians). Therefore we start from the phase signal, multiply it by 2*ma.PI to obtain radians, and compute the sine. The full program is the following:

Controlling the Frequency and Gain of the Oscillator

The next step is to add some controls for the frequency and gain of the oscillator. We can replace the fixed frequency 440 by a user interface slider:

process = osc(hslider("freq", 440, 20, 10000, 1));

and add a gain to control the output level of the oscillator:

process = osc(hslider("freq", 440, 20, 10000, 1)) * hslider("gain", 0.5, 0, 1, 0.01);

Adding a Gate Button

In order to prepare our MIDI synthesizer we need to add a gate button so that the sound is produced only when we press it:

process = osc(hslider("freq", 440, 20, 10000, 1)) * hslider("gain", 0.5, 0, 1, 0.01) * button("gate");

Adding an Envelope Generator

It is a good idea to also add an envelope generator. Here we will use a predefined ADSR in the standard Faust library.

Improving the Timbre

Instead of playing pure sine wave tones, let's improve the timbre with simple additive synthesis:

Running as a Polyphonic MIDI Synth

To control the synthesizer using MIDI you need to use Chrome. The polyphonic MIDI mode is activated using the drop down menu Poly Voices on the left side of the editor. Choose Computer Keyboard as MIDI input to play notes with the computer keyboard, or plug a MIDI keyboard.

Adding a Global Effect

A global effect can be added by providing a definition for effect.

// Common effect
effect = dm.zita_light;